Equation of a circle

Here you will learn about the equation of a circle, including how to recognize the equation of a circle, form an equation of a circle given its radius and center, use the equation of a circle to find its center and radius, and solve problems involving the equation of a circle.

Students will first learn about the equation of a circle as part of geometry in high school.

What is the equation of a circle?

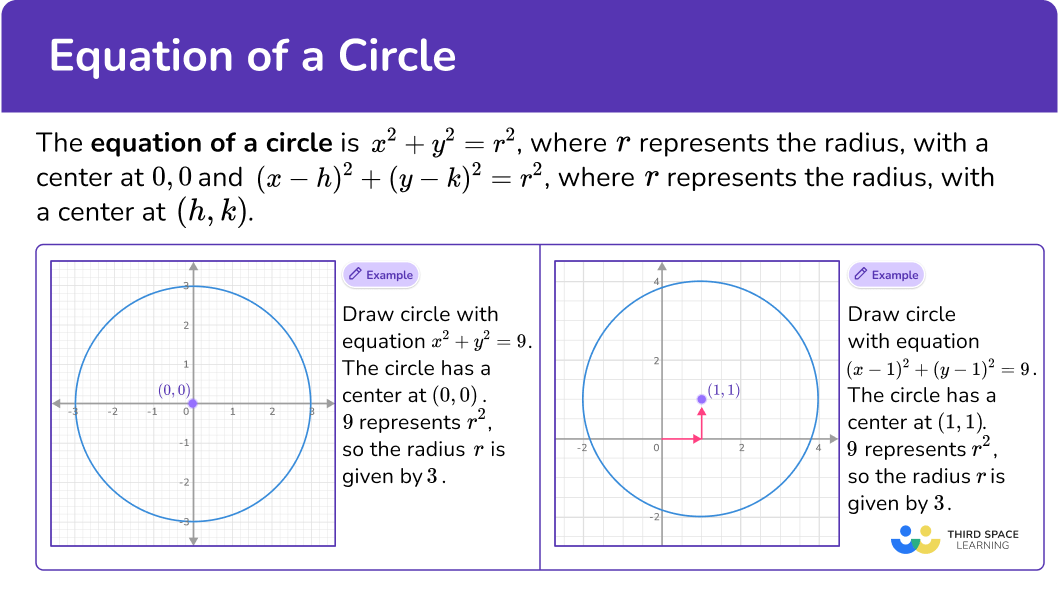
The equation of a circle is x^2+y^2=r^2, where r represents the radius, with a center at 0,0 and (x-h)^2+(y-k)^2=r^2, where r represents the radius, with a center at (h,k).

The definition of a circle is a set of all points on a plane that are a fixed distance from a center. That distance is called the radius.

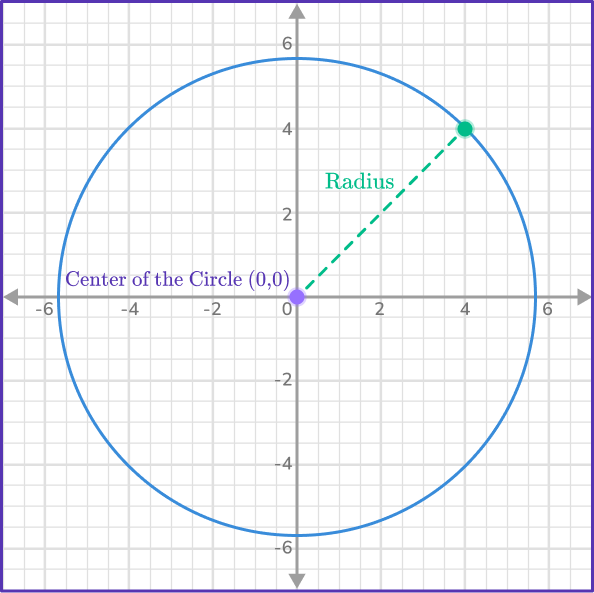
To understand the equation of a circle, consider the drawing below of a circle on a set of axes with the center at the origin.

Now consider a right angled triangle created when the radius of the circle is the hypotenuse of the right triangle.

• The horizontal line is the distance to the x coordinate
• The vertical line is the distance to the y coordinate
• The hypotenuse is the distance of the radius

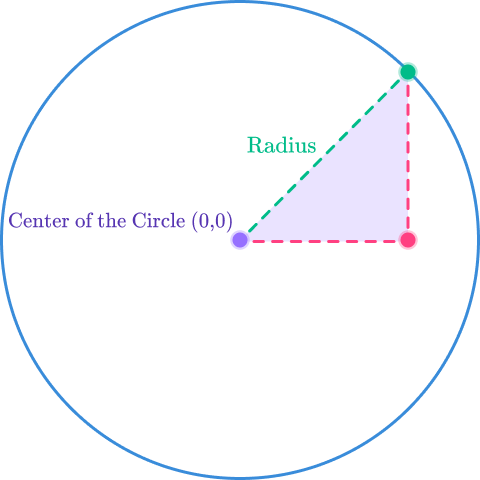
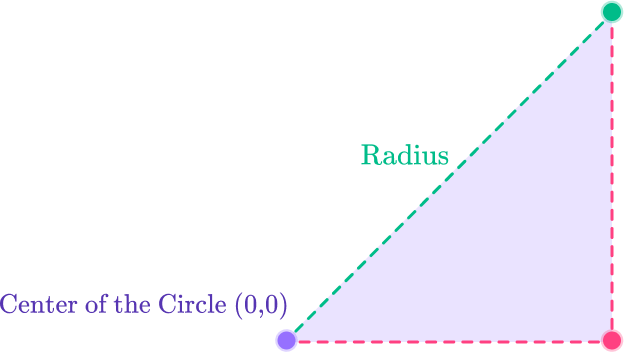
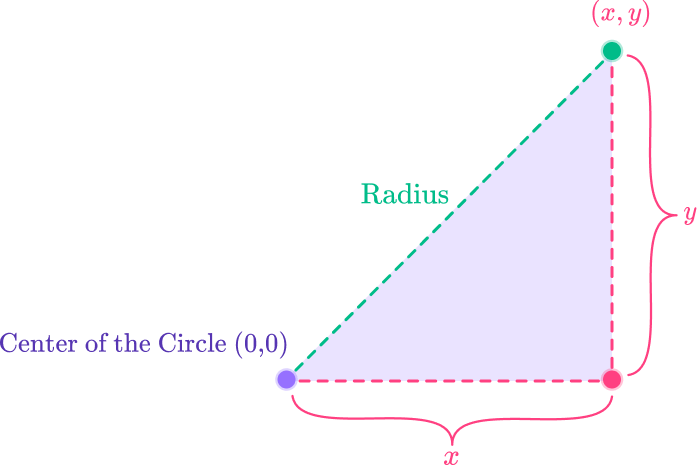
You can now apply Pythagoras’ theorem to the above. Therefore, the general form of the equation of a circle centered at (0,0) is:

x = x coordinate

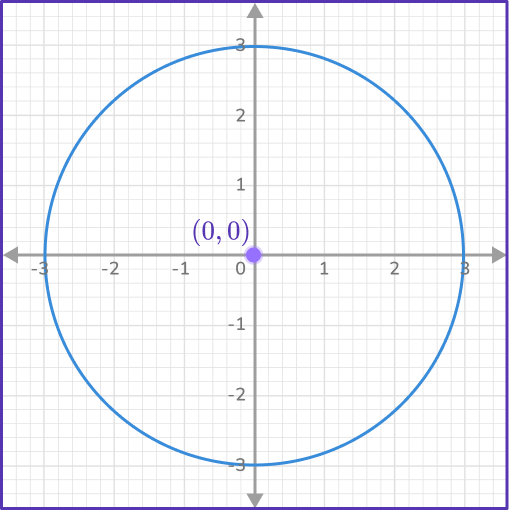
Draw circle with equation x^2+y^2=9.

The circle has a center at (0,0).

9 represents r^2, so the radius r is 3.

But what about a circle that is not centered on the origin? Let’s look at the same circle as above, but in a different position.

The radius of the circle below is still 3, but now the center is at (1,1). This means all the points on the circle have shifted up 1 and right 1.

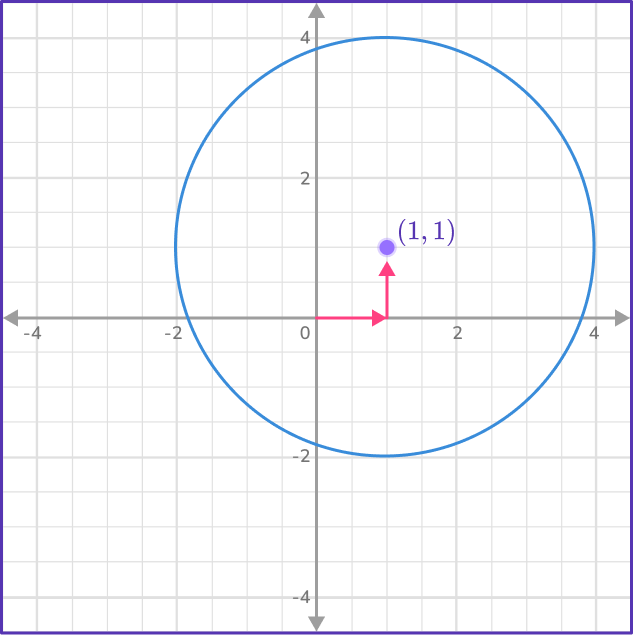
Since x^2+y^2=r^2 is true for all circles a (0,0), you can shift the circle back down to the origin.

To do that, you need to shift all the \textbf coordinates left \bf on the x- axis and shift all the \textbf coordinates down \bf on the y- axis to return this circle to the origin.

This leaves us with the equation (x-1)^2+(y-1)^2=9.

What about if this same circle was in another position?

The radius of the circle below is still 3, but now the center is at (-1,-1). This means all the points on the circle have shifted left 1 and down 1.

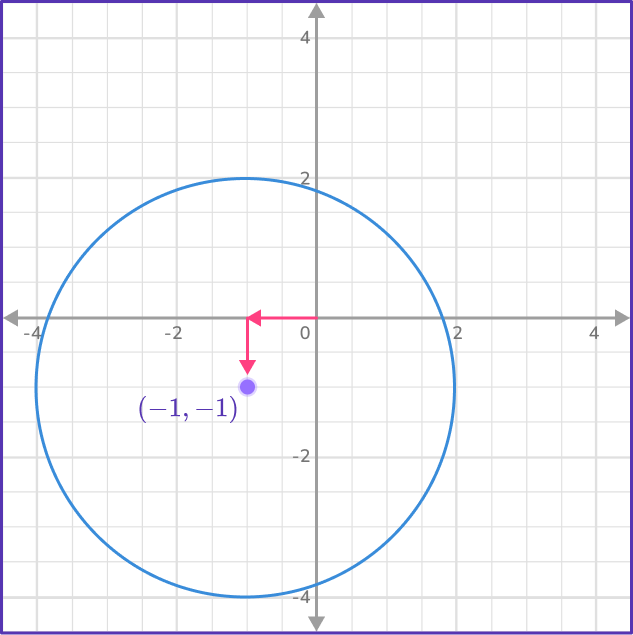
Since x^2+y^2=r^2 is true for all circles a (0,0), you need to shift all the \textbf coordinates right \bf and shift all the \textbf coordinates up \bf to return this circle to the origin. This leaves us with the equation (x+1)^2+(y+1)^2=9.

Therefore, the general form of the equation of any circle is:

h= x coordinate of center of the circle

k = y coordinate of center of the circle

r = radius of the circle

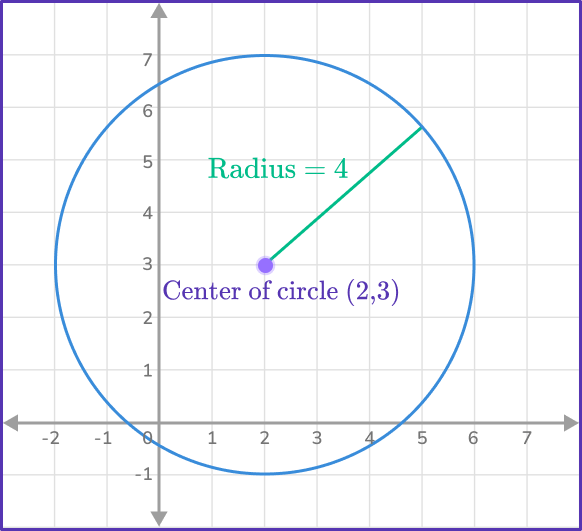
Draw the circle with equation (x-2)^2+(y-3)^2=4^2.

h = x coordinate of center = 2

k = y coordinate of center = 3

Coordinates of the center = (2,3)

r = length of radius = 4

What is the equation of the circle with a center of (2,5) and a radius of 10~?

The standard equation of a circle is (x-h)^2+(y-k)^2=r^2.

• The x -coordinate of center of the circle is 2
• The y -coordinate of the center of the circle is 5
• The radius is 10

What is the equation of a circle?

Common Core State Standards

How does this relate to high school math?

• Geometry – Expressing Geometric Properties with Equations (HSG.GPE.A.1)
  Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.

[FREE] Types of Graphs Check for Understanding Quiz (Grade 5 to 8)

Use this quiz to check your grade 5 to 8 students’ understanding of type of graphs. 15+ questions with answers covering a range of 5th to 8th grade type of graphs topics to identify areas of strength and support!

[FREE] Types of Graphs Check for Understanding Quiz (Grade 5 to 8)

Use this quiz to check your grade 5 to 8 students’ understanding of type of graphs. 15+ questions with answers covering a range of 5th to 8th grade type of graphs topics to identify areas of strength and support!

How to use the equation of a circle

In order to use the equation of a circle:

1. Write the general equation of a circle.
2. State any variables you know.
3. Substitute any values you know into the equation.
4. Use the information you have to solve the problem.
5. Clearly state the answer.

Equation of a circle examples

Example 1: writing the equation of a circle with center at the origin

What is the equation of the circle with a center at the origin?

1. Write the general equation of a circle.

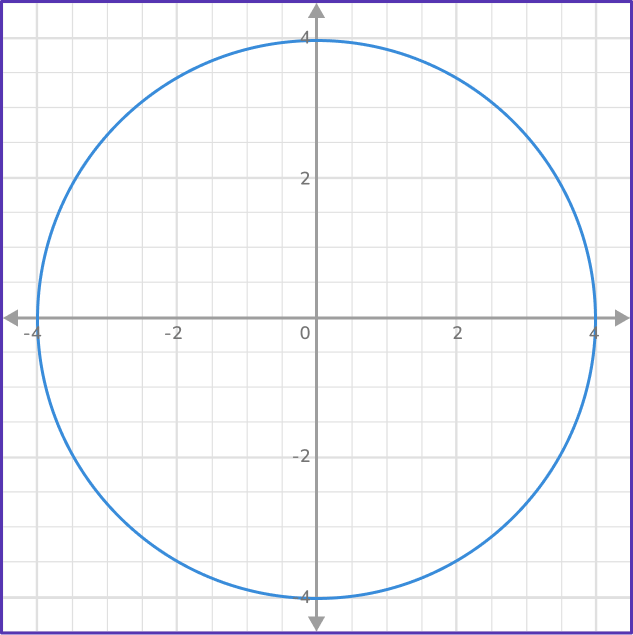
x^2+y^2=r^2 for circles at the origin.

2 State any variables you know.

The distance from the center (0,0) to the circle is 4.

3 Substitute any values you know into the equation.

4 Use the information you have to solve the problem.

Simplify the equation by squaring the radius.

5 Clearly state the answer.

The equation of the circle is: x^2+y^2=16

Example 2: finding the radius of a circle given its equation

What is the radius of the circle with the equation x^2+y^2=4?

Write the general equation of a circle.

x^2+y^2=r^2 for circles at the origin.

State any variables you know.

Radius, r, is unknown.

Equation of the circle is given as x^2+y^2=4.

Substitute any values you know into the equation.

You do not know any variables so we are unable to substitute here.

Use the information you have to solve the problem.

You know that the radius squared is equal to 4, so

Note: You only use the positive value as the radius’ measure of distance.

Clearly state the answer.